Mixed Solvent System
Mixed solvent systems
Solutions containing electrolytes and more than one solvent are often called “mixed solvent systems”. Mixed solvent systems containing one salt have been considered pseudo binary solutions consisting of “mixed solvent” and salt. This view makes it difficult to model “mixed solvent systems” because the standard chemical potentials of ions are functions of the solvent composition. It is necessary to know the numerical values of the standard chemical potentials of ions at the current solvent composition in order to perform solid-liquid equilibrium and liquid-liquid equilibrium calculations in such systems. With this approach, two models are actually required: one for the variation of the standard state properties with composition and another for the excess Gibbs function. The total Gibbs energy of a solution is the sum of the ideal solution Gibbs energy and the excess Gibbs energy. When the standard state properties are modified, the ideal part of the Gibbs energy changes. This change needs to be reflected in a similar change in the excess Gibbs energy also avoid discontinuities. An example of this type of modeling is the model by Pérez-Salado Kamps, “Model for the Gibbs Excess Energy of Mixed-Solvent (Chemical-Reacting and Gas-Containing) Electrolyte Systems, Ind. & Eng. Chem. Res., 44(2005)201-225, DOI:10.1021/ie049543y.
A more straightforward method for modeling mixed solvent systems is presented here. This method makes it possible to calculate solid-liquid-equilibria, vapor-liquid equilibria, and liquid-liquid equilibria with great accuracy using the same set of parameters using the relatively simple thermodynamic model, the Extended UNIQUAC model. Some results of this type of modeling are shown below. It is based on two basic thermodynamic concepts:
- Choice of standard states: Water is considered to be the solvent, electrolytes and non-electrolytes are solutes. The standard state for all solutes is the aqueous standard state. Standard state properties as Gibbs energy of formation and enthalpy of formation are therefore not dependent on composition. Thus no additional model for the standard state properties is required.
- Modeling the effect of the variation of the relative permittivity with composition: The relative permittivity (electric constant) is used for calculating the electrostatic contribution to the interaction between ions in an aqueous solution. It can be determined experimentally that the relative permittivity varies with the solution composition. The effect of solutes on the activity of other components in the solution, including the variation of the relative permittivity, is accounted for through the energy interaction parameters in the excess Gibbs function.
This method for modeling mixed solvent electrolyte solutions was described in the following publications, which also contain the required model parameters:
- Kaj Thomsen and Peter Rasmussen, Modeling of vapor – liquid – solid Equilibria in gas – aqueous electrolyte systems, Chemical Engineering Science Vol. 54(1999)1787-1802, DOI:10.1016/S0009-2509(99)00019-6
- Maria Iliuta, Kaj Thomsen and Peter Rasmussen, Extended UNIQUAC model for correlation and prediction of vapour-liquid-solid equilibria in aqueous salt systems containing non-electrolytes . Part A. Methanol – water – salt systems, Chemical Engineering Science, 55(2000)2673-2686, DOI:10.1016/S0009-2509(99)00534-5
- Kaj Thomsen, Maria Iliuta, and Peter Rasmussen, Extended UNIQUAC model for correlation and prediction of vapor-liquid-liquid-solid equilibria in aqueous salt systems containing non-electrolytes. Part B. Alcohol (Ethanol, Propanols, Butanols) – water – salt systems. (Chemical Engineering Science 59(2004)3631-3647, issue 17), DOI:10.1016/j.ces.2004.05.024
- Kaj Thomsen, Martin Due Olsen, Lucas FF Corrêa, Modeling vapor-liquid-liquid-solid equilibrium for acetone-water-salt systems, Pure and Applied Chemistry (2020) https://doi.org/10.1515/pac-2019-1013
Solubility of potassium sulfate in mixed solvent systems
The following six systems are considered on this page:
- Methanol-K2SO4-H2O at 60°C
- Ethanol-K2SO4-H2O at 25°C
- 1-Propanol-K2SO4-H2O at 45°C
- i-Propanol-K2SO4-H2O at 50°C
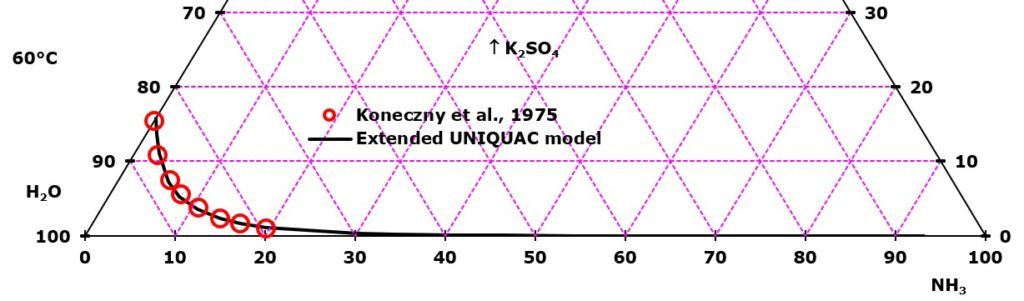
- NH3-K2SO4-H2O at 60°C
- Acetone-K2SO4-H2O at 35°C
The phase diagrams below show solubility isotherms for these six systems. The solubility isotherms describe compositions of each system in equilibrium with solid potassium sulfate. In all these systems, K2SO4 is being salted out by the addition of non-electrolytes. ‘Salted out’ means that the solubility decreases and an excess of salt precipitates.
Of the six non-electrolytes added one by one in each of the six diagrams, ammonia has a stronger salting out effect on K2SO4 than the four alcohols and acetone. In all the depicted phase diagrams, the markers represent experimental data while the solubility equilibrium lines were calculated with the Extended UNIQUAC model. Notice that the temperatures vary between the diagrams.
In all the graphs below, the focus is on the lower part of the diagrams. The apex with pure K2SO4 is therefore not shown. All compositions are in mass %. The mass percent of K2SO4 can be read on the right axis in all the diagrams
K2SO4 solubility in methanol-water mixtures. The experimental data plotted in the diagram are from
- Chmarzynski, The system K2SO4-MgSO4-H2O-CH3OH at 60°C, Chemia Stosowana, 21(1977)195-202
- Chmarzynski, Equilibrium studies of the K2SO4-H2O-CH3OH system at temperatures 298.15, 308.15, 323.15, and 333.15K, Chemia Stosowana, 33(1989)261-268
- Koneczny, Lango, and Lango, Badania ukladu K2SO4-NH3-H2O, Chemia Stosowana, 19(1975)27-36
K2SO4 solubility in ethanol-water mixtures. The experimental data plotted in the diagram are from
- Armstrong and Eyre, Studies of the processes operative in solutions. XL – The displacement of salts from solutions by various precipitants, Phil. Trans. Royal Soc. London. Ser. A. Physical Sciences and Eng., 84(1910)123-136
- Fox and Gauge, The Solubility of Potassium Sulphate in Concentrated Aqueous Solutions of Non-Electrolytes, J. Chem. Soc., 97(1910)377-385
- Tomaszewski and Wasowska, Potassium sulfate-magnesium sulfate-water system in the presence of ethanol at 25°C, Chemia Stosowana, 19(1975)437-444 (4)
K2SO4 solubility in 1-propanol-water mixtures. The experimental data plotted in the diagram are from Taboada, Véliz, Galleguillos, and Graber, Solubilities, Densities, Viscosities, Electrical Conductivities, and Refractive Indices of Saturated Solutions of Potassium Sulfate in Water + 1-Propanol at 298.15, 308.15, and 318.15 K, J. Chem. Eng. Data, 47(2002)1193-1196, https://doi.org/10.1021/je020024g
K2SO4 solubility in 2-propanol-water mixtures. The experimental data plotted in the diagram are from Mydlarz, J., Jones, A. G., Millan, A., Solubility and Density Isotherms for Potassium Sulfate-Water-2-Propanol, J. Chem. Eng. Data, 34(1989)124-126; https://doi.org/10.1021/je00055a033
K2SO4 solubility in ammonia-water mixtures. The experimental data plotted in the diagram are from Koneczny, Lango, and Lango, Badania ukladu K2SO4-NH3-H2O, Chemia Stosowana, 19(1975)27-36
K2SO4 solubility in acetone-water mixtures. The experimental data plotted in the diagram are from Mydlarz and Jones, Potassium Sulfate Water-Alcohols Systems: Composition and Density of Saturated Solutions, J. Chem. Eng. Data, 35(1990)214-216; https://doi.org/10.1021/je00060a036
The Extended UNIQUAC modeling of the aqueous acetone system was published in Modeling vapor-liquid-liquid-solid equilibrium for acetone-water-salt system, Pure and Applied Chemistry (2020), https://doi.org/10.1515/pac-2019-1013
Liquid-Liquid-Equilibrium in the iso-propanol – sodium sulfate – water system
Water and iso-propanol are miscible in all proportions. A miscibility split can be caused by a number of salts. One of them is sodium sulfate. The phase diagram below shows experimental data for liquid-liquid equilibrium in the isopropanol – Na2SO4 – H2O system at 35°C. The experimental data were measured by Lynn et al. (ref. 1). The phase diagram shows the binodal curve calculated with the Extended UNIQUAC model together with the experimental data.
The model parameters used for the calculation are those from Thomsen et al. (ref. 2). The calculation was performed with the multi-phase flash (VLLSE) routine developed by Aqueous Solutions Aps and implemented in a DLL callable from Microsoft Excel.
- Lynn, S., Schiozer, A. L., Jaecksch, W. L., Cos, R., Prausnitz, J. M., “Recovery of anhydrous Na2SO4 from SO2-scrubbing liquor by extractive crystallization: liquid-liquid equilibria for Aqueous Solutions of Sodium Carbonate, Sulfate, and/or Sulfite Plus Acetone, 2-Propanol, or tert-Butyl Alcohol”, Ind. Eng. Chem. Res., 35(1996)4236-4245, DOI:10.1021/ie960094e.
- Thomsen, Kaj; Iliuta, Maria; and Rasmussen, Peter, “Extended UNIQUAC model for correlation and prediction of vapor-liquid-liquid-solid equilibria in aqueous salt systems containing non-electrolytes. Part B. Alcohol (Ethanol, Propanols, Butanols) – water – salt systems”. (Chemical Engineering Science 59(2004)3631-3647, issue 17), DOI:10.1016/j.ces.2004.05.024.